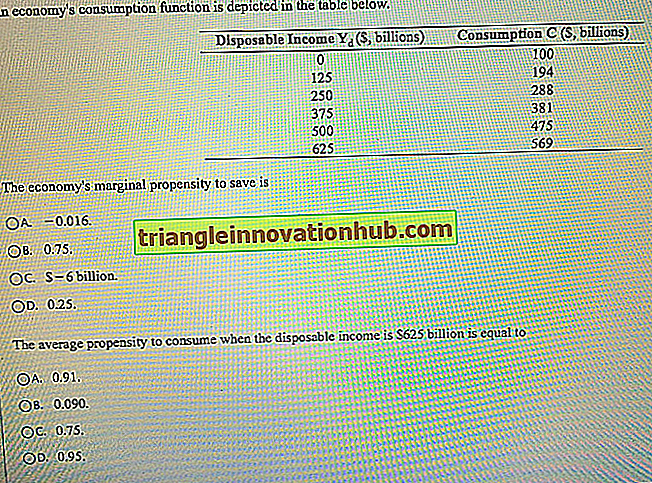
Måling av variabilitet: En oversikt

Måling av variabilitet: En oversikt!

Betydning av variabilitet:

Variabilitet betyr "Scatter" eller "Spread". Dermed kan variasjonsmålinger referere til spredning eller spredning av score rundt sin sentrale tendens. Tiltakene av variabilitet indikerer hvordan fordelingen sprer seg over og under sentrale anbud.

Fra følgende eksempel kan vi få en klar ide om begrepet mål for variabilitet:

Anta at det er to grupper. I en gruppe er det 50 gutter og i en annen gruppe 50 jenter. En test blir administrert til begge disse gruppene. Den gjennomsnittlige poengsummen til gutter og er 54, 4, og jenter er vi sammenligner gjennomsnittlig poengsum for begge gruppene, vi finner at det ikke er noen forskjell i de to gruppene. Men antar at guttens poeng er funnet å variere fra 20 til 80, og jenters score varierer fra 40 til 60.

Denne forskjellen i rekkevidde viser at guttene er mer variable, fordi de dekker mer territorium enn jentene. Hvis gruppen inneholder personer med vidt forskjellige kapasiteter, vil resultatene bli spredt fra høy til lav, området vil være relativt bredt og variabiliteten blir stor.

Denne situasjonen kan illustreres grafisk i figurene nedenfor:

Ovenstående figur viser to frekvensfordeling av det enkelte området (N) og noen gjennomsnitt (50), men med svært forskjellig variabilitet. Gruppe A varierer fra 20 til 80 og gruppe B fra 40 til 60 Gruppe A er tre ganger så variabel som gruppe-B-Spreads over tre ganger avstanden på skalaen av score-skjønt begge fordelingene har den sentrale tendensen.

Definisjoner av variabilitet:

Ordbok for utdanning-CV bra. " Spredning eller variabilitet av observasjoner av en fordeling om noe mål av sentral tendens." Collins Dictionary of Statistics: "Dispersjon er spredningen av en fordeling"

AL Bowley:

"Dispersjon er måling av variasjonen av elementene."

Brooks og Dicks:

"Dispersjon eller spredning er graden av spredning eller variasjon av variablene om en sentral verdi." Således er egenskapen som angir i hvilken grad verdiene er dispergert om de sentrale verdier, kalt dispersjon. Det indikerer også mangelen på ensartethet i størrelsen på gjenstander av en distribusjon.

Behov for variabilitet:

1. Hjelper til å bestemme avviksforanstaltninger:

Tiltakene av variabilitet hjelper oss å måle graden av avvik, som finnes i dataene. Av det kan bestemme grenser innenfor hvilke dataene vil marine i noe målbart utvalg eller kvalitet.

2. Det hjelper å sammenligne ulike grupper:

Ved hjelp av tiltak av gyldighet kan vi sammenligne de opprinnelige dataene uttrykt i forskjellige enheter.

3. Det er nyttig å supplere informasjonen gitt av tiltakene av sentral tendens.

4. Det er nyttig å beregne ytterligere forhåndsstatistikk basert på spredningstiltakene.

Variabilitetsmålinger:

Det er fire målinger av variabilitet:

1. Utvalget

2. Kvartilavviket

3. Gjennomsnittlig avvik

4. Standardavviket

Disse er:

1. Utvalget:

Range er forskjellen mellom i en serie. Det er det mest generelle målet for spredning eller spredning. Det er et mål for variasjoner av varianter eller observasjon blant seg selv og gir ikke en ide om spredningen av observasjonene rundt noen sentral verdi.

Område = H-L

Her H = Høyeste poengsum

L = Laveste poengsum

Eksempel:

I en klasse har 20 studenter sikret merkene som følger:

22, 48, 43, 60, 55, 25, 15, 45, 35, 68, 50, 70, 35, 40, 42, 48, 53, 44, 55, 52

Her-Den høyeste poengsummen er 70

Laveste poeng er 15

Område = H - L = 70-115 = 55

Hvis området er høyere enn gruppen indikerer mer heterogenitet, og hvis området er lavere enn gruppen indikerer mer homogenitet. Dermed gir området oss en umiddelbar og grov indikasjon på variasjonen i en distribusjon.

Meriter av Range:

1. Område er lett beregnet og lett forstått.

2. Det er den enkleste måten å variere.

3. Det gir et raskt estimat av variasjonsmålet.

Demerits of Range:

1. Spekteret er sterkt påvirket av svingning av score.

2. Det er ikke basert på alle observasjonene i serien. Det tar bare de høyeste og laveste poengene i kontoen.

3. I tilfelle av åpne sluttfordeler kan ikke rekkevidde brukes.

4. Det påvirkes sterkt av svingninger i prøvetaking.

5. Det påvirkes sterkt av ekstreme score.

6. Serien er ikke virkelig representert etter rekkevidde. En symmetrisk og en symmetrisk fordeling kan ha samme område, men ikke den samme spredning.

Bruk av rekkevidde:

1. Område brukes som et mål for spredning når variasjoner i verdien av variabelen ikke er mye.

2. Område er det beste måleområdet for variabilitet når dataene er for spredte eller for lite.

3. Spekter brukes når kunnskap om ekstremt poengsum eller total spredning er ønsket.

4. Når et raskt estimat av variabilitet er ønsket rekkevidde benyttes.

2. Kvartilavviket (Q):

Ved siden av rekkevidde kvartilavvik er et annet mål for variabilitet. Det er basert på intervallet som inneholder de midt femti prosent av tilfellene i en gitt distribusjon. Et fjerdedel betyr 1/4 av noe, når en skala er delt inn i fire like deler. "Kvartilavviket eller Q er halvparten av skalaen mellom 75 og 25 prosentene i en frekvensfordeling."

Fra figur 9.2 fant vi at 1. kvartil eller Q ₁ er posisjon i en fordeling under hvilke 25% tilfeller, og over hvilke 75% tilfeller ligger. Den andre kvartilen eller Q2 er en posisjon under og over hvilke 50% tilfeller ligger. Det er medaljene i fordelingen.

Den tredje kvartilen eller Qg er den 75. prosentilen, under hvilke 75% tilfeller og over hvilke 25% tilfeller ligger. Så kvartilavviket (Q) er en halv avstandsskalaene mellom 3. kvartil (Q ₃ ) og 1. kvartil (Q ₁ ). Det er også kjent som Semi-Interquartile Rage.

symbolsk:

Derfor har vi for å beregne kvartilavvik først og fremst å beregne 1. kvartil (Q ₁ ) og 3. kvartil (Q ₃ )

Hvor = L = Nedre grense for den første kvartil-klassen,

Den første kvartil-klassen er den klassen, hvis kumulative frekvens er større enn verdien av N / 4 når hvis beregnes fra nedre ende.

N / 4 = En fjerdedel av det totale antall tilfeller.

F = Kumulativ frekvens av klasseintervallet under

1. kvartil klasse.

Fq ₁ = Frekvensen av Q _1- klassen

i = Størrelsen på klasseintervallet 3N

Hvor: L = Nedre grense for 3. kvartilklasse

Den tredje kvartil-klassen er den klassen hvis kumulative frekvens (Cf) er større enn verdien av 3N / 4 dvs. Cf> 3N / 4, når Cf beregnes fra nedre ende.

3N / 4 = ¾ av N eller 75% av det totale antall tilfeller.

F = Kumulativ frekvens av klassen under klassen.

fq ₂ = Frekvensen av Q _3- klassen.

i = Størrelsen på klasseintervallet.

Beregning av kvartil fra gruppedata:

Eksempel:

Finn ut kvartilavviket fra følgende data:

Fremgangsmåte for å beregne kvartilavvik:

Trinn 1:

Beregn N / 4 dvs. 25% av fordelingen og 3N / 4 dvs. 75% av fordelingen.

Her -N = 50 så N / 4 = 12, 5

og 3N / 4 = 37, 5

Steg 2:

Beregn C f fra nedre enden. Som i tabell 9.1 kolonne-3.

Step-3:

Finn ut Q ₁ og Q _3- klassen.

I dette eksemplet:

Ci, 60-64 er Q1 klasse fordi C f > N / 4

Ci 75-79 er Q ₃ klasse fordi

Cf> 3N / 4

Step-4:

Finn ut F for Q ₁ klasse og Q ₃ klasse. I dette eksemplet

F for Q ₁ klasse = 10

F for Q3 klasse = 30 Trinn

Trinn 5:

Finn ut Q1 ved å sette de ovennevnte verdiene i formel.

Q ₁ = L + N / 4 - F / fq1 xi

Her L = 59, 5 fordi de eksakte grensene for Q _1- klassen 60-64 er 59, 5-64, 5.

F = 10 Cf under Q _1- klassen

Fq ₁ = 4: Den nøyaktige frekvensen av Q _1- klassen

i = 5, størrelsen på klasseintervallet

N / 4 = 12, 5

Nå Q ₁ = 59, 5 + 12, 5-10 / 4 x 5

= 59, 5 + 2, 5 / 4 x 5

= 59, 5 + 0, 63 x 5

= 59, 5 + 3, 13 = 62, 63

Trinn 6:

Finn ut Q ₃ ved å sette verdiene i formel.

Her L = 74, 5 fordi de nøyaktige grensene for Q _3- klassen 75-79 er 74, 5-79, 5.

F = 30 Cf under Q _3- klassen.

3N / 4 = 37, 5

Fq ₁ = 8 den nøyaktige frekvensen av Q _3- klassen.

i = 5 størrelsen på klassens intervaller.

Q3 = 74, 5 + 37, 5-30 / 8 x 5

= 74, 5 + 7, 5 / 8 x 5 = 74, 5 + .94 x 5

= 74, 5 + 4, 7 = 79, 2

Trinn 7:

Finn ut Q ved å sette ovenstående verdi i formel.

Q = Q3-Q1 / 2 = 79, 2 - 62, 63 / 2

= 16, 5 / 2 = 8, 285 = 8, 29

Fortjeneste av kvartilavvik:

1. Kvartilavvik er enkel å beregne og lett å forstå.

2. Det er mer representativt og tillit verdig enn rekkevidde. I tilfelle av åpne intervaller i klassen, brukes den til å studere tiltak av spredning.

3. Ved klassifiseringsintervaller med åpen slutt brukes den til å studere tiltak av dispersjon.

4. Det er en god indeks av poengtetthet i midten av distribusjonen.

5. Når vi tar median som mål for sentral tendens på den tiden, er Q foretrukket som mål for dispersjon.

6. Like rekkevidde er det ikke påvirket av ekstreme score.

Demerits av kvartilavvik:

1. Det er ikke basert på alle observasjoner av data. Den ignorerer de første 25% og de siste 25% av resultatene.

2. Videre algebraisk behandling er ikke mulig i tilfelle Q. Det er bare et posisjonelt gjennomsnitt. Det studerer ikke variasjon av verdiene av en variabel fra noe gjennomsnitt. Det viser bare en avstand på en skala.

3. Det påvirkes av svingning av poeng. Verdien er i alle fall påvirket av en verdiendring av en enkelt poengsum.

4. Q er ikke et egnet mål for spredning, når det i en serie er en betydelig variasjon i verdiene til forskjellige poeng.

Bruk av kvartilavvik:

1. Når Median er målet for sentral tendens på den tiden, Q blir brukt, brukes som mål for dispersjon.

2. Når ekstreme score påvirker SD eller resultatene er spredt på det tidspunktet, blir Q brukt som mål for variabilitet.

3. Når vår primære interesse er å vite konsentrasjonen rundt medianen - den midterste 50% av tilfellene, på den tiden Q blir brukt.

4. Når klassens intervaller er åpne, blir Q brukt som mål for dispersjon.

3. Gjennomsnittlig avvik (AD):

Vi har diskutert om to variabilitet, rekkevidde og kvartilavvik. Men ingen av disse dispersjonene angir sammensetningen av fordelingen. Det er fordi begge dispersjonene ikke tar hensyn til alle individuelle score. Vi kan overvinne noen av de alvorlige manglene i rekkevidde og kvartilavvik ved å bruke en annen dispersjon kalt gjennomsnittlig avvik eller gjennomsnittlig avvik.

"Gjennomsnittlig avvik er det aritmetiske gjennomsnittet av alle avvikene fra forskjellige score fra gjennomsnittsverdien av resultatene uten hensyn til tegnet av avviket."

Dermed er gjennomsnittlig avviks aritmetisk gjennomsnitt av avvikene i en serie beregnet fra noe mål av sentral tendens. Så gjennomsnittlig avvik er gjennomsnittet av avvikene tatt fra deres gjennomsnittlige (Noen ganger fra median og modus.)

definisjoner:

Collins Dictionary of Statistics:

"Gjennomsnittlig avvik er gjennomsnittet av de absolutte verdiene av forskjellene mellom verdiene til en variabel og gjennomsnittet av dens fordeling."

Ordbok for utdanning, CV Bra:

"Et mål som uttrykker det gjennomsnittlige beløpet som de enkelte elementene i en fordeling avviker fra et mål på sentral tendens, som gjennomsnittet av medianen."

HE Garrett:

"Gjennomsnittlig avvik eller AD er gjennomsnittet av avvikene til alle separate poeng i en serie tatt fra deres gjennomsnitt (av og til fra medianen eller modusen)."

Således kan det sies at gjennomsnittlig avvik eller gjennomsnittlig avvik som den kalles er gjennomsnittet av avvikene til alle poengene.

Det tas ingen hensyn til tegn og alle avvik enten + ve eller -ve har blitt behandlet som positiv.

hvor AD = gjennomsnittlig avvik

£ = Capital Sigma, Middel Summen av

II = Modulert kort sagt Mod, betyr ingen respekt for negativt tegn.

x = avvik, (X-M)

Beregning av gjennomsnittlig avvik:

Det er to situasjoner for beregning av gjennomsnittlig avvik:

(a) Når data er ugruppert.

(b) Når data er gruppert.

Beregning av AD fra ugrupperte data.

Eksempel:

Finn AD av de følgende 10 poengene gitt nedenfor:

23, 34, 16, 27, 28, 39, 45, 26, 18, 27

Løsning:

Trinn 1:

Finn ut gjennomsnittet av resultatene med formel

AX / N

Steg 2:

Finn ut avvik fra alle score som trekker gjennomsnittet fra resultatene.

Step-3:

Finn ut absolutt avvik som vist i tabell 9.2 og deretter Σ | x |

Step-4:

Sett verdiene i formel.

AD = 7, 58.

Beregning av AD fra grupperte data:

Eksempel:

Finn ut AD av følgende data:

Løsning :

Trinn 1:

Finn ut gjennomsnittet av fordelingen.

Mean = 70.80

Steg 2:

Finn ut midtpunktet for hver klasseintervall. Som i kolonne -3 i tabell -9.3

Step-3:

Finn ut x ved å trekke gjennomsnittet fra midtpunktet (X). Som vist i kolonne -5 i tabell 9.3.

Step-4:

Finn ut absolutt avvik eller | x |. Som kolonne -6 ovenfor.

Step-5:

Finn ut | f x |. ved å multiplisere f med | x. Som vist i kolonne -7 og finn ut Σ | f x |.

Step-6:

Sett de ovennevnte verdiene i formel.

Formelen for AD fra grupperte data

Hvor = AD = Gjennomsnittlig avvik

Σ = Summen av

f = frekvens

x = avvik, dvs. (X-M)

N = Totalt Antall tilfeller ie Σ f .

Setter verdiene i formel

Meriter av AD:

1. Gjennomsnittlig avvik er stift definert og verdien er presis og bestemt.

2. Det er lett å beregne.

3. Det er lett å forstå. Fordi det er gjennomsnittet av avvikene fra et mål på sentral tendens.

4. Det er basert på alle observasjonene.

5. Det er mindre påvirket av verdien av ekstreme score.

Demerits av AD:

1. Den mest alvorlige ulempen med gjennomsnittlig avvik er at den ignorerer de algebraiske tegnene på avvikene som er imot grunnleggende regler for matematikk.

2. Videre algebraisk behandling er ikke mulig i tilfelle AD.

3. Det brukes svært sjelden. På grunn av standardavvik brukes vanligvis som et mål for dispersjon.

4. Når det beregnes fra modusen AD, gir ikke nøyaktig måling av dispersjon.

Bruk av gjennomsnittlig avvik:

1. Gjennomsnittlig avvik brukes når det er ønskelig å vekt alle avvikene fra gjennomsnittet i henhold til deres størrelse.

2. Når ekstreme score påvirker standardavviket på den tiden, er AD det beste målet for spredning.

3. AD brukes når vi ønsker å vite hvorvidt tiltakene er spredt ut på hver side av gjennomsnittet.

4. Standardavviket (SD):

Vi har diskutert tre målinger av variabilitet nemlig Range, Quartile Deviation og Average Deviation. Vi har også funnet ut at alle av dem lider av alvorlige ulemper.

Utvalget bare tatt inn for å bare regne med høyeste poengsum og laveste poengsum. Kvartilavviket tar bare hensyn til de midterste 50% av resultatene og i tilfelle av gjennomsnittlig avvik ignorerer vi skiltene.

Derfor for å overvinne alle disse vanskelighetene bruker vi et annet mål for spredning som kalles Standard Deviation. Det brukes ofte i eksperimentell forskning, da det er den mest stabile variabelenes indeks. Symbolisk er det skrevet som σ (gresk liten bokstav sigma).

definisjoner:

Collins ordbok for statistikk.

"Standardavvik er et mål for spredning eller spredning. Det er root mean squared avvik. "

Ordbok for utdanning-CV bra.

"En mye brukt måling av variabilitet, som består av kvadratroten av middelverdien av de kvadrerte avvikene fra score fra gjennomsnittet av fordelingen."

Standardavviket er kvadratroten av gjennomsnittsverdien av de kvadrerte avvikene fra resultatene fra deres aritmetiske gjennomsnitt.

SD-verdien beregnes ved å oppsummere den kvadratiske avviket fra hvert mål fra gjennomsnittet, dividert med antall tilfeller og utvinning av kvadratroten. For å være tydeligere, bør vi merke seg at ved beregning av SD setter vi alle avvikene separat, finner summen deres, deler summen med totalt antall poeng, og deretter finner vi kvadratroten av gjennomsnittet av kvadrert avvik. Slik at det også kalles "rotmiddelkvadratavviket".

Firkanten av standardavviket kalles Varians (σ ² ). Det refereres til som gjennomsnittlig kvadratfeil. Det kalles også som andre øyeblikksdispersjon.

Beregning av SD fra uoppfordret data:

Eksempel:

Finn ut SD av følgende data:

6, 8, 10, 12, 5, 8, 9, 17, 20, 11.

Løsning:

Trinn 1:

Finn ut gjennomsnittet av resultatene.

Steg 2:

Finn ut avvik (x) av hver poengsum.

Beregning av SD fra grupperte data:

I gruppert data kan SD beregnes i to metoder:

1. Direkte metode eller lang metode

2. Kort metode eller antatt gjennomsnittlig metode

1. Direkte metode eller lang metode:

Eksempel:

Finn ut SD av følgende distribusjon:

Løsning:

Trinn 1:

Finn ut midtpunktet for hvert klasseintervall. (Colum-3 Tabell 9.4)

Steg 2:

Finn ut gjennomsnittet av fordelingen:

Her M = Σ f x / N = 3540/50

= 70, 80

Trinn -3:

Finn ut avviket (x) ved å trekke gjennomsnittet fra poeng.

Trinn -4:

Finn ut f x ved å multiplisere f (kol-2) med x (kol-5)

Step-5:

Finn ut f x ved å multiplisere f x (col-2) med x (kol-5)

Step-6:

Beregn Σ f x ved å legge til verdiene i kol-7.

Step-7:

Sett verdiene i formel.

2. Kort metode eller antatt metode:

Kort sagt, beregning av SD er enkelt og mindre tidkrevende. Hvis midtpunktene i klassens intervaller er desimaltall, blir det mer komplisert å beregne SD i lang metode. Denne metoden består i hovedsak av å gjette, eller antar en gjennomsnittlig og senere å anvende en korreksjon for å gi reelt middel. Slik at det kalles som antatt gjennomsnittlig metode.

Eksempel:

Beregn SD, med følgende fordeling:

Løsning:

Trinn 1:

Anta midtpunktet for et hvilket som helst klasseintervall som "antatt middel". Men det er bedre å anta midtpunktet av klassens intervall i midten med høyest frekvens som antatt gjennomsnitt. Her antas det å være = 72 som antatt å bety.

Steg 2:

Finn ut x (avvik av scoreene fra antatt gjennomsnitt) som vist i kol-3.

x '= X - M / i

Step-3:

Beregn f x ', ved å multiplisere x' med f (kol-4).

Step-4:

Beregn f x ² ved å multiplisere x '(kol-3) med f x (col-5).

Step-5:

Finn ut Σ f x 'og Σ f x ' ² det 'ved å legge til verdiene i kol-4 og kol-5 henholdsvis. '

Step-6:

Sett verdiene i formel:

Formel for SD i kort metode er:

Hvor jeg = Størrelsen på klasseintervallet

Σ = Summen av

f = frekvens

x '= avvik av scoreene fra deres antatte gjennomsnitt.

Nå hvis vi skal erstatte Σ f x '/ N i stedet for C.

Formelen vil være som følger:

Nå legger vi verdiene i formel.

1. Hvis en konstant verdi legges til hver poengsum eller subtraheres fra hver poengsum, forblir valsen av SD uendret:

Det betyr at SD er uavhengig av opprinnelsesendring (tillegg, subtraksjon). Således dersom en konstant verdi legges til eller subtraheres fra hver variasjon, forblir SD det samme.

Vi kan undersøke dette fra følgende eksempel:

I tabellen over er det gitt 5 studenter. La oss se hva som skjer med SD av resultatene hvis vi legger til et konstant tall si 5 og trekk 5 fra hver score.

2. Hvis en konstant verdi multipliseres eller deles opp til de opprinnelige resultatene, blir også verdien av SD multiplisert med eller delt med samme nummer:

Det betyr at SD er uavhengig av skalaforandring (multiplikasjon, divisjon). Hvis vi multipliserer de opprinnelige resultatene med et konstant tall, blir også SD-verdien multiplisert med det samme nummeret.

Igjen dersom vi deler hver poengsum med et konstant tall, blir også SD'en delt med det samme nummeret.

Vi kan illustrere dette med følgende eksempel:

I tabellen over er det gitt 5 studenter. La oss se hva som skjer med SD av de 5 resultatene hvis vi multipliserer det med et konstant nummer, si 2 og del det med samme konstante tall.

Dermed fra dette fant vi ut at hvis antallene blir multiplisert med et konstant tall, blir σ også multiplisert med det. Hvis poengene er delt med et konstant tall, blir σ også delt med samme nummer.

Meriter av SD:

1. Standardavvik er fast definert og verdien er alltid bestemt.

2. Det er basert på alle observasjoner av data.

3. Det er i stand til videre algebraisk behandling og har mange matematiske egenskaper.

4. I motsetning til Q og AD er det mindre påvirket av fluktuasjoner av score.

5. I motsetning til AD, ignorerer den ikke de negative tegnene. Ved kvadratering av avvik overvinne den disse vanskelighetene.

6. Det er det pålitelige og mest nøyaktige måleområdet for variabilitet. Det går alltid med det som er det mest stabile målet for sentral tendens.

7. SD gir et mål som er sammenlignbar mening fra en test til en annen. Fremfor alt uttrykkes de normale kurveenheter i en enhet.

Demerits of SD:

1. SD er vanskelig å forstå og ikke lett å beregne.

2. SD gir mer vekt til ekstreme score og tap til de som er nærmere den gjennomsnittlige. Det er fordi kvadratene av avvikene, som er store i størrelse, vil være forholdsmessig større enn kvadratene til de avvikene som er forholdsvis små.

Bruk av SD:

1. SD brukes når vår trekk er å måle variabiliteten som har størst stabilitet.

2. Når ekstreme avvik kan påvirke variabiliteten på den tiden, brukes SD.

3. SD brukes til å beregne ytterligere statistikk som korrelasjonskoeffisient, standardpoeng, standardfeil, variasjonsanalyse, analyse av kovariasjon etc.

4. Når tolkning av score er gjort i form av NPC, brukes SD.

5. Når vi vil bestemme pålitelighet og gyldighet av testresultater, brukes SD.

Kombinert standardavvik:

Under forskningsarbeidet tegner vi noen ganger mer enn en prøve fra befolkningen. Derfor får vi forskjellige SD-er for hver gruppe eller prøve. Men noen ganger må vi tolke disse resultatene som en gruppe. Derfor, når forskjellige sett av poeng er blitt kombinert til et enkelt parti, er det mulig å beregne SD av totalfordelingen fra SD-gruppene i undergruppene.

Formel for beregning kombinert standardavvik eller er som følger: